JS 代码
根据以下代码实现 TaskPro ,类似洋葱模型
js
// 实现 TaskPro 类
class TaskPro {}
// 使用
const t = new TaskPro()
t.addTask(async (next) => {
console.log('1-start')
await next()
console.log('1-end')
})
t.addTask((next) => {
console.log('2')
next()
})
t.addTask((next) => {
console.log('3')
next()
})
t.run() // 1-start , 2 , 3 , 1-endTaskPro 类实现
js
class TaskPro {
#taskList = []
addTask(task) {
this.#taskList.push(task)
}
run() {
const task = this.#taskList.shift()
return task(() => {
if (this.#taskList.length === 0) return
return this.run()
})
}
}虚拟 dom 转真实 dom
js
const vnode = {
tag: 'DIV',
attrs: {
id: 'app'
},
children: [
{
tag: 'SPAN',
children: [
{
tag: 'A',
children: ['router', 'link']
}
]
},
{
tag: 'SPAN',
children: [
{
tag: 'A',
children: ['go']
},
{
tag: 'A',
children: []
}
]
}
]
}关键 api
document.createElement(tagName)新建domele.setAttribute(attr, value)设置attr属性parent.appendChild(ele)子元素放置
js
const render = (vnode) => {
const toDom = (node, parent = null) => {
// 文本
if (typeof node === 'string' && parent) {
parent.innerText += node
return parent
}
// 标签
const { tag, attrs, children } = node
const ele = document.createElement(tag.toLowerCase())
// 处理 attrs
if (attrs) {
Object.keys(attrs).forEach(key => {
ele.setAttribute(key, attrs[key])
})
}
// 处理 子元素
if (children && children.length) {
children.forEach(child => {
toDom(child, ele)
})
}
// 父级挂载
if (parent) {
parent.appendChild(ele)
} else {
parent = ele
}
return parent
}
const dom = toDom(vnode)
return dom
}
// 测试
render(vnode)版本号排序
输入一组版本号,输出从大到小的排序
js
const versions = ['2.1.0.1', '0.402.1', '10.2.1', '5.1.2', '1.0.4.5']
const versionSort = (list) => {
return list.sort((v1, v2) => {
let i = 0
const arr1 = v1.split('.')
const arr2 = v2.split('.')
while(true) {
// 取出同位置数字
const s1 = arr1[i]
const s2 = arr2[i]
i++
// 其中一个小版本号空了,则比较完毕
if (s1 === undefined || s2 === undefined) {
return arr2.length - arr1.length
}
// 相同则继续对比下一个小版本号
if (s1 === s2) continue
// 否则比较 小版本数字大小
return s2 - s1
}
})
}
versionSort(versions) // ['10.2.1', '5.1.2', '2.1.0.1', '1.0.4.5', '0.402.1']二分查找
双指针从两端向中间查找目标值的位置
js
const list = [1, 2, 3, 4, 5, 6, 9, 10, 88]
const findIndex = (arr, target) => {
let left = 0, right = arr.length - 1
while(left <= right) {
const mid = Math.floor((left + right) / 2)
if (arr[mid] > target) {
right = mid - 1
} else if (arr[mid] < target) {
left = mid + 1
} else {
return mid
}
}
return -1
}文件大小单位转换
将文件的 KB 单位简化,保留两位小数,例如 1024KB => 1024MB
js
const formatSizeUnit = (kb) => {
const units = ['KB', 'MB', 'GB', 'TB', 'PB']
let index = 0
while(kb >= 1024 && index < units.length - 1) {
kb /= 1024
index++
}
return `${kb.toFixed(2)} ${units[index]}`
}
formatSizeUnit(1024)数组 转 树
使用 map 来缓存 id 和 对应的数组元素 id -> treeItem , 遍历时判断 map 中是否存在 parentId 对应的 id , 存在则将 treeItem 保存到 parentItem.children 中
js
const list = [
{ id: 1, name: '部门A', parentId: 0 },
{ id: 2, name: '部门B', parentId: 1 },
{ id: 3, name: '部门C', parentId: 1 },
{ id: 4, name: '部门D', parentId: 2 },
{ id: 5, name: '部门E', parentId: 3 },
{ id: 6, name: '部门F', parentId: 3 },
];
const convertArrToTree = (arr) => {
let root = null;
const idMap = new Map();
arr.forEach((item) => {
// tree item
const { id, parentId, name } = item;
const treeItem = { id, name };
// 缓存
idMap.set(id, treeItem);
// 找到 parent 并 push 到 children
const parentItem = idMap.get(parentId);
if (parentItem) {
if (parentItem.children === undefined) {
parentItem.children = [];
}
parentItem.children.push(treeItem);
}
// 是根节点的话赋值给 root
if (parentId === 0) {
root = treeItem;
}
});
return root;
}
console.log(convertArrToTree(list));排序
冒泡排序
两层遍历,注意遍历范围,相邻元素进行比较交换位置
复杂度
O(n²),稳定排序算法
js
const list = [2, 4, 1, 666, 23, 12, 67, 99]
const bubbleSort = (arr) => {
// 外层 遍历 控制排序进行多少轮
for(let i = 0; i < arr.length; i++) {
// 内层 遍历 控制相邻的数据比较
for(let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 前一个比后一个大,则交换位置
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
}
}
}
return arr
}选择排序
两层遍历,每次遍历找到剩余元素中的最小值,选择最小值插到已排序的元素后面
复杂度
O(n²),不稳定排序算法
js
const list = [2, 4, 1, 666, 23, 12, 67, 99]
const selectSort = (arr) => {
// 剩余中最小值的下标
let minIndex
// 外层 遍历 控制排序进行多少轮
for(let i = 0; i < arr.length; i++) {
minIndex = i
// 从当前指针开始 找小于当前的 最小的 值
for(let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
// 遍历找到最小的值的下标
minIndex = j
}
}
// 如果剩余最小值的下标不是当前指针,则交换
if (minIndex !== i) {
[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
}
}
return arr
}插入排序
取剩余元素第一个元素作为目标元素,往前遍历已排序的元素并移动,找到比目标元素小的,则插入到目标元素后面
复杂度
O(n²),稳定排序
js
const list = [2, 4, 1, 666, 23, 12, 67, 99]
const insertSort = (arr) => {
// 从第二个元素开始遍历
for (let i = 1; i < arr.length; i++) {
let p = i
// 记录要插入的目标元素
const target = arr[p]
// 从 target 所在位置向前遍历,直到找到一个比目标元素小的,然后插在后面
while(p > 0 && arr[p - 1] > target) {
// 移动前一个元素到下一个位置
arr[p] = arr[p - 1]
p--
}
arr[p] = target
}
return arr
}快速排序
使用递归,将中间元素放置在新数组中间,比中间元素大的放右边,小的放左边
时间复杂度为
O(nlogn),不稳定排序
js
const list = [2, 4, 1, 666, 23, 12, 67, 99]
const quickSort = (arr) => {
// 递归结束条件
if (arr.length <= 1) return arr
// 中间节点
const mid = Math.floor(arr.length / 2)
// 以中间节点为基准,比中间大的放 right ,小的 放 left
const base = arr.splice(mid, 1)[0] // 先移除中间节点
const left = [], right = []
for (const item of arr) {
if (item > base) {
right.push(item)
} else {
left.push(item)
}
}
// 递归,重新组合数组,base 重新放置在 中间
return [...quickSort(left), base, ...quickSort(right)]
}打乱数组 - 洗牌算法
长度为 n 的数组的全排列有 n! 种,也就是说打乱结果总共有 n! 种。
洗牌算法,产生的结果必须有 n! 种可能,否则无法做到真的打乱了。
js
// 遍历数组,将每个元素与后面的随机元素交换
const nums = [1, 2, 3, 4, 5]
const shuffle = (arr) => {
const n = arr.length
for (let i = 0; i < n; i++) {
const r = Math.floor(i + Math.random() * (n - i))
// 交换
const t = arr[i]
arr[i] = arr[r]
arr[r] = t
}
return arr
}二叉树遍历
广度优先遍历
队列(先进后出), 每个节点都需将左右子节点从右边入队,遍历时从左边出队
js
const breadthFirst = (root) => {
const arr = [];
if (!root) return arr;
// 维护队列
const stack = [root];
while(stack.length) {
// 出队
const node = stack.shift();
arr.push(node.val);
// 入队
node.left && stack.push(node.left);
node.right && stack.push(node.right);
}
return arr;
}深度优先遍历
递归,类似前序遍历
js
const arr = [];
const depthFirst = (root) => {
if (!root) return arr;
arr.push(root.val);
root.left && depthFirst(root.left);
root.right && depthFirst(root.right);
}
arr;层序遍历
递归,注意要先遍历完一层,才能进行下一层遍历,返回值应该是一个二维数组,分别用于储存每一层的节点值
js
const levelOrder = (root) => {
const arr = []
if (!root) return arr
const stack = [root]
while(stack.length) {
let len = stack.length
// 一层一个数组临时储存
const tmp = []
while(len--) {
const node = stack.shift()
tmp.push(node.val)
// 按顺序 入队
node.left && stack.push(node.left)
node.right && stack.push(node.right)
}
// 遍历完一层,push 进 arr
arr.push(tmp)
}
}滑动窗口最大值
给定一个数组 nums ,有一个大小为 k 的滑动窗口,从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口中的 k 个数字。滑动窗口每次只向右移动一位,求返回 滑动窗口中的最大值
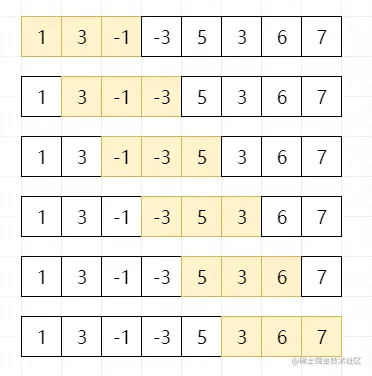
js
const nums = [1, 3, -1, -3, 5, 3, 6, 7], k = 3
const maxSlideWindow = (nums, k) => {}最长递增子序列
一个整数数组 nums ,找到其中一组最长递增子序列的值
买卖股票
字符串所有排列组合
输入一个字符串,打印出该字符串中,所有字符的排列组合
js
const str = 'abc'
const combine = () => {}